
The inactivated poliovirus vaccine (IPV) developed by Jonas Salk was licensed for use in 1955. This vaccine consists of the three serotypes of poliovirus whose infectivity, but not immunogenicity, is destroyed by treatment with formalin. When prepared properly, IPV does not cause poliomyelitis (early batches of IPV were not sufficiently inactivated, leading to vaccine-associated outbreaks of polio, the so-called Cutter incident). From 1955 to 1960 cases of paralytic poliomyelitis in the United States dropped from 20,000 per year to 2,500.
While Salk’s vaccine was under development, several investigators pursued the production of infectious, attenuated vaccines as an alternative. This approach was shown to be effective by Max Theiler, who in 1937 had made an attenuated vaccine against yellow fever virus by passage of the virulent virus in laboratory mice. After many passages, the virus no longer caused disease in humans, but replicated sufficiently to induce protective immunity. Albert Sabin capitalized on these observations and developed attenuated versions of the three serotypes of poliovirus by passage of virulent viruses in different animals and cells. In contrast to Theiler’s yellow fever vaccine, which was injected, Sabin’s poliovirus vaccines were designed to be taken orally – hence the name oral poliovirus vaccine (OPV). As in a natural poliovirus infection, Sabin’s vaccines would replicate in the intestinal tract and induce protective immunity there and in the bloodstream.
Sabin began testing his attenuated vaccines in humans in 1954. By 1957 there was evidence that the virus that was fed to volunteers was not the same as the virus excreted in the feces. As Sabin writes:
It was evident, however, that as in the young adult volunteers, the virus in some of the stool specimens had a greater neurovirulence than the virus originally swallowed in tests in monkeys.
What Sabin did not know was whether the change in neurovirulence of his vaccine strains constituted a threat to the vaccine recipients and their contacts, a question that could only be answered by carrying out larger clinical trials. Many felt that such studies were not warranted, especially considering the success of IPV in reducing the number of paralytic cases. Sabin notes that his friend Tom Rivers, often called the father of American virology, told him to ‘discard the large lots of OPV that I had prepared into a suitable sewer’.
Despite the opposition to further testing of OPV in the US, others had different views. An international committee of the World Health Organization recommended in 1957 that larger trials of OPV should be carried out in different countries. Sabin’s type 2 vaccine was given to 200,000 children during an outbreak of polio in Singapore in 1958, and follow-up studies revealed no safety problems. In Czechoslovakia 140,000 children were given OPV and subsequent studies revealed that the virus spread to unimminized contacts but did not cause disease.
Perhaps the most important numbers came from trials of OPV in the Soviet Union. Sabin had been born in Russia and had close contacts with Soviet virologists, including Mikhail Chumakov, director of the Poliomyelitis Research Institute in Moscow. Chumakov was not satisfied with the results of IPV trials in his country and asked Sabin to send him OPV for testing. By the end of 1959 nearly 15,000,000 people had been given OPV in different parts of the Soviet Union with no apparent side effects. Dorothy Horstmann, a well known virologist at Yale University, was sent to the Soviet Union to evaluate the outcome of the trials. Horstmann writes:
It was clear that the trials had been carefully carried out, and the results were monitored meticulously in the laboratory and in the field. By mid-1960 approximately 100 million persons in the Soviet Union, Czechoslovakia, and East Germany had received the Sabin strains. Of great importance was the demonstration that the vaccine was safe, not only for the recipients, but for the large numbers of unvaccinated susceptible who must have been exposed as contacts of vaccines.
The results obtained from these trials in the Soviet Union convinced officials in the US and other countries to carry out clinical trials of OPV. In Japan, Israel, Chile, and other countries, OPV was shown to be highly effective in terminating epidemics of poliomyelitis. In light of these findings, all three of Sabin’s OPV strains were approved for use in the US, and in 1961-62 they replaced IPV for routine immunization against poliomyelitis.
As soon as OPV was used in mass immunizations in the US, cases of vaccine-associated paralysis were described. Initially Sabin decried these findings, arguing that temporal association of paralysis with vaccine administration was not sufficient to implicate OPV. He suggested that the observed paralysis was caused by wild-type viruses, not his vaccine strains.
A breakthrough in our understanding of vaccine-associated paralysis came in the early 1980s when the recently developed DNA sequencing methods were used to determine the nucleotide sequences of the genomes of the Sabin type 3 vaccine, the neurovirulent virus from which it was derived, and a virus isolated from a child who had developed paralysis after administration of OPV. The results enumerated for the first time the mutations that distinguish the Sabin vaccine from its neurovirulent parent. More importantly, the genome sequence of the vaccine-associated isolate proved that it was derived from the Sabin vaccine and was not a wild-type poliovirus.
We now understand that every recipient of OPV excretes, within a few days, viruses that are more neurovirulent that the vaccine strains. This evolution occurs because during replication of the OPV strains in the human intestine, the viral genome undergoes mutation and recombination that eliminate the attenuating mutations that Sabin so carefully selected by passage in different hosts.
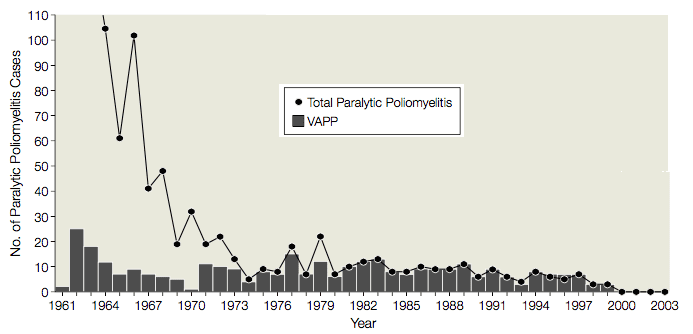
From 1961 to 1989 there were an average of 9 cases (range, 1-25 cases) of vaccine-associated paralytic poliomyelitis (VAPP) in the United States, in vaccine recipients or their contacts, or 1 VAPP case per 2.9 million doses of OPV distributed (illustrated). Given this serious side effect, the use of OPV was evaluated several times by the Institute of Medicine, the Centers for Disease Control and Prevention, and the Advisory Committee on Immunization Practices. Each time it was decided that the risks associated with the use of OPV justified the cases of VAPP. It was believed that a switch to IPV would lead to outbreaks of poliomyelitis, because: OPV was better than IPV at protecting non-immunized recipients; the need to inject IPV would lead to reduced compliance; and IPV was known to induce less protective mucosal immunity than OPV.
After the WHO began its poliovirus eradication initiative in 1988, the risk of poliovirus importation into the US slowly decreased until it became very difficult to justify routine use of OPV. In 1996 the Advisory Committee on Immunization Practices decided that the US would transition to IPV and by 2000 IPV had replaced OPV for the routine prevention of poliomyelitis. As a consequence VAPP has been eliminated from the US.
OPV continues to be used in mass immunization campaigns for the WHO poliovirus eradication program, because it is effective at eliminating wild polioviruses, and is easy to administer. A consequence is that neurovirulent vaccine-derived polioviruses (VDPV) are excreted by immunized children. These VDPVs have caused outbreaks of poliomyelitis in areas where immunization coverage has dropped. Because VDPVs constitute a threat to the eradication campaign, WHO has recommended a global transition to IPV. Once OPV use is eliminated, careful environmental surveillance must be continued to ensure that VDPVs are no longer present before immunization ceases, a goal after eradication of poliomyelitis.
As a virologist working on poliovirus neurovirulence, I have followed the vaccine story since I joined the field in 1979. I have never understood why no cases of VAPP were observed in the huge OPV trials carried out in the Soviet Union. Had VAPP been identified in these trials, OPV might not have been licensed in the US. Global use of OPV has led to near global elimination of paralytic poliomyelitis. Would the exclusive use of IPV have brought us to the same point, without the unfortunate cases of vaccine-associated paralysis? I’m not sure we will ever know the answer.
Update: As recently as 1997 DA Henderson, architect of smallpox eradication, argued that developed countries should not use IPV, because it ‘implies accepting the potential of substantial penalties while reducing but not eliminating, an already extremely small risk of vaccine-associated paralytic illness’.

Great! I just listened to TWiV 191: When two rights make a wrong the other day, and this article completes the story on a scientific level. With less than 1 VAPP case per million doses distributed, it seems natural that OVP was the vaccine of choice, even though it complicates final eradication efforts. OVP has doubtlessly saved millions of contracting polio, and this would logistically have been impossible using IPV.
My personal opinion is that the OPV should have been phased out decades ago. We can talk about slight increase in cost, and a need to inject but that is true for most vaccines. No one bothers with oral version of other vaccines to increase compliance or greater muscosal immunity. The fact remains that the IPV is also highly effective.
The key is that the risk needed to be modeled on a continuous/updated basis, because at some point the OPV will have a higher risk profile (also given the aforementioned differences in compliance etc.) than the IPV in a given region.
The OPV for example was phased out in Australia several decades too late.
“Less than 1 VAPP per million doses distributed”, yes and it is not pretty when you see it first hand. Just like the effects of the wild virus…
It is my understanding that IPV prevents spread of the virus to the nervous system, but does not prevent replication of virus in the gut. If everyone starts immunizing with IPV, won’t potentially revertant vaccine virus potentially keep circulating for decades in kids’ unprotected guts? I don’t see how we get to a point where we can stop vaccinating, even if we hit zero symptomatic infections. Unless we come up with a vaccine that induces gut immunity and can’t revert (eg codon deoptimized virus)…
You are correct, IPV does not immunize the gut. However the results of a new study indicate that children who have received OPV respond to an inoculation with IPV with an increase in mucosal immunity. Therefore it could be that a switch to IPV will not be accompanied by as dramatic an increase in the number of susceptible intestines. Perhaps in time this will result in a decay of circulating OPV strains. See https://virology.ws/2015/01/06/an-unexpected-benefit-of-inactivated-poliovirus-vaccine/
I do understand your concerns, but the fact is that IPV was never used to the extent that OPV was, and there was concern that it simply could not stop outbreaks in the same way. We’ll never really know if IPV could have done the job.
I thought I understood what was going on here, but this piece now confuses me a bit. I had thought that the vaccine derived casualties were of unimmunised children who came into contact with the faeces of recently OPV treated contacts. Now you seem to be saying that the person actually treated sometimes becomes a casualty too! Would you clarify for me, and in the piece: are those who become ill after they themselves are treated, becoming ill through some direct effect of the vaccine in their digestive tract, or; are they becoming ill later through contact with their own faeces, or; is this just a drafting error, and those given the vaccine do not actually appear in the vaccine damaged statistics? If the vaccine recipient is at risk from their own faeces: how long before they are immune?
Presumably: there need not be many of these further cases, if proper hygiene was possible and carried out. Or are there still some people who do have reactions to the OPV itself?
It seems nothing is ever perfectly clear.
Vaccine-associated polio in the vaccine recipient is caused by the vaccine replicating and reverting to neurovirulence in the intestine, from which it spreads to the nervous system. It has nothing to do with contamination with feces. Thus, hygiene has no effect. The only way to avoid vaccine-associated paralysis is to stop using OPV (or to first give a dose of IPV, then OPV, but then we are using two vaccines which is too costly and complicated).
However there are some cases of vaccine-associated paralysis that occur in contacts of the vaccine recipients. These are usually parents changing the diapers of their recently vaccinated children. Having changed diapers myself, I see no good way to avoid contamination with a kicking, moving child. Maybe latex gloves would help but most don’t have those.
Sorry it wasn’t clear. I have written a lot about VAPP on this blog and did not want to repeat it – I should have linked to some of the articles.
Thanks very much for clarifying. I had not appreciated how quickly the potent virus could be recreated, and had assumed that the bulk of the modern cases were from unvaccinated people’s contact with faeces.
How long would it take for an OPV recipient to be immune from the repotentiated virus in their own gut? (ie.: What is the latest time after vaccination that an OPV recipient has succumbed to VAPP?).
Many thanks.
GPEI nonetheless is going for one IPV before switching to bOPV. The irony, I take it, is obvious.
This depends to some extent on how one defines VAPP, because it has to be teased out of all cases of acute flaccid paralysis (one may not have timely stool samples). It appears that 4–40 days has become a sort of canonical window; see, e.g., here.
Because there is not a new version can replace it.
Sanitation and hygiene do matter. Were the children in Mali and Ukraine recently stricken with vaccine-derived polio vaccinated? Moreover, what’s to stop a significant percentage of those vaccinated from becoming carriers of mutated vaccine viruses, shedding the virus in water-based sanitation systems? “since the virus can be spread through feces, if there’s inadequate sanitation, sewage mixed with the water supply might be another possible route for transmission.”
http://www.npr.org/sections/goatsandsoda/2015/09/10/434647957/how-did-polio-pop-up-in-two-polio-free-countries-ukraine-and-mali
What an excellent overview, thank you. RE: “I have never understood why no cases of VAPP were observed in the huge OPV trials carried out in the Soviet Union.” Perhaps like wild polio, VDPV is asymptomatic, explained by balance in the viral-bacterial microbiome where exposure to certain bacteria dramatically increase polio infectivity. This paper found exposure to the bacterium B. cereus increased polio infectivity 500x:
“Intestinal microbiota promote enteric virus replication and systemic pathogenesis”
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3222156/?hc_location=ufi
Indeed, this new paper found viruses that infect bacteria, not human cells, were the most rich and diverse earliest in an infant’s life:
“Early life dynamics of the human gut virome and bacterial microbiome in infants”
http://www.nature.com/nm/journal/vaop/ncurrent/full/nm.3950.html
Thanks Boris: this is an aspect I had not picked up on, and, really ought to have appreciated when trying to argue with the ‘vaccination shy’.
Cheers.
Because it is more effective than other vaccines.-Antibody Sequencing
Apropos of this, the Lancet last week reported the results of a five-arm immunogenicity trial with IPV (after OPV). One thing that really stood out to me (which may be in the associated comment) is that tOPV is scheduled to disappear worldwide within a two-week period in 2016.
Pingback: Polio Vs Cancer - Were You Informed? - For Bangun Omah
Interesting to note that vaccine associated neurotropic or viscerotropic diseases caused by yellow fever live vaccine is higher than that of OPV [YFV=1.3 cases per 1 million doses (Kitchener S. Viscerotropic and neurotropic disease
following vaccination with the 17D yellow fever vaccine,
ARILVAX. Vaccine 2004; 22:2103–2105] vs. OPV=1 case per 2.9 million doses of OPV distributed], still there is no incentive to switch to inactivated YF vaccine due to commercial reasons.
Im confused. If the CDC states that up to 98% of Wild Type Polio is asymptomatic with no symptoms, and about 1% get VAPP from the vaccine, how is that so much better? We see 48,000+ cases of VAPP in the Indians after vaccinations with OPV that were not included in surveillance or investigated?
Do the same changes that make the virus more neuropathic also cause it to become predominant within the gut? I was just wondering how that selection operates.
Pingback: 26 AUG 1906-3 MAR 1993 ALBERT SABIN – heveblog
Pingback: Three countries endemic for poliovirus
” I have never understood why no cases of VAPP were observed in the huge OPV trials carried out in the Soviet Union.” Really?
haha funny comment
Wishful thinking I guess.lol
What I’ve never understood is why they don’t give a Salk vaccine shot, then for the booster, give the Sabin vaccine. In particular I say this because: has anyone ever checked to see what fraction of baby boomers who have chronic fatigue syndrome have had the sabin and not the Salk? I’m one of the older Sabin only persons and have had CFS symptoms since about 1962. In particular it seems to me that CFS resembles the syndrome that people who’ve had a mild polio case frequently develop as an adult.
I wonder if the reason no app was seen in Soviet union was because the oral polio vaccine was different with stronger strains less xusceltzble to mutation